Mathematical Logic – Part 1

Mathematical logic

Mathematical logic is the foundation of all mathematics. Of course, you probably know this, but before you skip ahead, a small note. I think you haven’t seen it laid out like this before. All circuits, but everyday communication, operate based on mathematical logic, and I will illustrate this with examples. Let’s get started, as it will be lengthy. The first major topic is advanced mathematics.

Without any explanation, I bet you already know some basic logical operations, and you use them every day:

• OR
• AND
• NOT

But these are just words: yes and no. Words with deeper meanings—and now, let’s dive into a little philosophy!

Honey, after your workout, could you swing by the store and grab tomatoes and arugula for the salad? If you’d like, we could also add some Parmesan cheese or tuna to make it even tastier!

Sounds simple, right? But wait! Let’s steer this message into philosophical territory and start asking questions:

• What if the store has NEITHER tomatoes NOR arugula?
• If there’s NEITHER tomatoes NOR arugula, should I get cheese OR tuna?
• If there are tomatoes AND arugula, but NO cheese, should I NOT get tomatoes AND arugula EITHER?

You could probably continue this line of reasoning for quite a while. I highlighted the NEITHER, OR, AND words on purpose. While I call them words, we need to expand their meanings if we want to venture further into philosophy. They now must be seen as operations. AND and OR, NOT articulate clear operations. To unlock the screen lock on our phone, the last AND the penultimate password characters must match, and you can either love OR hate math, but when it comes to a vodka martini, we ask for it shaken, NOT stirred. Yet, for Mr. Bond to receive the right drink at every pub in the world, several centuries, even millennia, had to pass. Like so many things, it all started with the Greeks!

Back to the time – the birth of logic

The first name we must mention is none other than the father of logic himself, Aristotle (384 BCE – 322 BCE). He authored numerous works on logic, which his followers compiled around 50 BCE under the title (translated: tool). Aristotle regarded logic as the most fundamental and essential tool; without it, the pursuit of science and philosophy is impossible!

What really matters to us now is one part of the , namely the Prior Analytics, which deals with conclusions (), and the Posterior Analytics, which focuses on logical proofs. This foundational knowledge sets the stage for all logical reasoning and critical thinking that follows. So strap in, because we’re embarking on a journey through the intellect of one of history’s greatest minds!

Let’s dive into the Three Laws of Thought:

1. Every entity is identical to itself.
2. No entity is identical to its opposite.
3. Between a thing and its denial, only one can be true.

We also need to mention the principle of double inference:

Socrates is a man. All men are mortal. Therefore, Socrates is mortal.

How logical is that? Sure, when it’s laid out like this, it’s easy to see, but we had to travel this far to get here. Now, let’s make a huge leap through time and space and not stop until we reach the Misty Isles of Albion…

The next name on my list is George Boole (1815-1864), the self-taught English mathematician and philosopher. In 1847, he published his groundbreaking work, , which presented the algebraic system of logic.

Boole didn’t see logic as merely a branch of mathematics; instead, he highlighted the clear analogy between algebraic symbols and those used in the description of logic. And once we have a descriptive language, statements can be transformed into equations.

The philosophical concepts of AND, OR, and NOT were now given a mathematical foundation, although, at that time, this hardly piqued the interest of many—resulting in a stagnation of the development of mathematical logic due to a lack of attention. But the seeds of a revolution in logical thought had been sown, waiting for the right moment to bloom!

Boole’s work was carried forward by his English colleague, Augustus De Morgan (1806-1871), who made a splash first with (coming soon!), and later became famous for the identities that bear his name:

1. Identity:
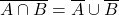
2. Identity:

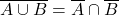
I know this might not mean much at first glance:

1. Identity: The complement of the intersection is equal to the union of the complements.
2. Identity: The complement of the union is equal to the intersection of the complements.

But don’t worry, you’re about to unravel the mystery behind these statements and discover the beauty of logical relationships!

The work of Boole and De Morgan represented an intriguing area of mathematics at the end of the 1800s, with minimal practical applicability. For roughly 70 years, progress stalled, but then came the technological advancements following World War II, which led to a remarkable rediscovery of mathematical logic. It was during this era that the power of logical reasoning began to transform industries, paving the way for innovations in computing and artificial intelligence. The world was on the brink of a logic revolution!

In the 1940s, American communications engineer Claude Elwood Shannon (1916-2001) stumbled upon Boole’s work during his philosophical studies. At the time, he was writing his doctoral thesis on designing electrical circuits. That’s when the idea struck him: by leveraging the mathematical foundations laid down by Boole, he could optimize the system of electrical relays. Furthermore, he became the first to physically construct logical circuits using electronic components!

Who would have thought that mathematical logic could lead to such groundbreaking advancements? Especially, if we give some extraordinary talent scientists from Hungary...

Boolean algebra—the foundations of mathematical logic:

To start, let’s get acquainted with some essential concepts:

• Truth Table: A comprehensive table that outlines all possible input combinations for a logical operation and their corresponding output responses. To keep things manageable in our first topic, I’ll present a model with two logical variables.
• Logical (input) Variable: A logical operation can have any number of logical variables associated with it—these represent the input side. Imagine standing in front of an ATM. The keypad has numbers from zero to nine and several operation buttons allowing us to confirm, edit, or delete. In total, there are 13 logical variables on this keypad. We can input data and initiate operations.
• Logical (input) Value: The logical value is simply the value a logical variable can take. Sticking with our previous example, each numbered button contains 1 digit, while each operation button triggers a pre-programmed action when pressed. Input isn’t limited to buttons; a whole family of sensors is at our disposal, like the volume control on your headphones!
• High Value: 1 or TRUE (let’s NOT think of this as a number in mathematical logic…)
• Low Value: 0 or FALSE
• Output Value / Statement: The result of the logical operation for the given logical (input) values. The term ‘statement’ can also be used when examining the truth value of assertions or propositions.

Now, let’s dive into the mathematical part. As I mentioned, we will only be working with the model of 2 logical variables here and now. What do you think—how many possible logical operations can be created with 2 logical variables?

Yes, the correct answer is 16!

To keep it simple, let me provide two statements:

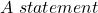• – The math lecture is a bore.
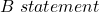• – I’ll sing.

1.Possibility – Contradiction

Designation:

Equation: or

We have a contradiction when a statement is simultaneously TRUE and FALSE, which makes it meaningless: ‘The math lecture is boring AND not boring.’ This logical relationship is also known as the principle of NONCONTRADICTION. The output value is always zero, regardless of the input values…

Cases	A	B
1	0	0	0
2	0	1	0
3	1	0	0
4	1	1	0

2. Possibility – Tautology

Designation:

Equation: or

A tautology is a statement that is always true—in other words, it’s a statement that attempts to explain itself, like this: ‘A math lecture is a boring OR not boring ..’ This logical relationship is also known as ALWAYS. The output is consistently one, reinforcing the inescapable truth within the statement!

Cases	A	B
1	0	0	1
2	0	1	1
3	1	0	1
4	1	1	1

3. Possibility – TRUE statement for A

Designation:

Equation:

In this context, the TRUE statement for A means that ‘The math lecture is boring,’ and we agree, but it’s cold outside, so we’re staying. It’s important to note that we do not invoke statement B—because if I were to start singing, the lecture would no longer be boring…

Cases	A	B
1	0	0	0
2	0	1	0
3	1	0	1
4	1	1	1

4. Possibility – NOT TRUE statement for A

Designation:

Equation: or

The NOT TRUE statement regarding A is simply the negation of the previous assertion, meaning ‘the math lecture is NOT boring.’ This logical relationship is known as NEGATION. From now on, I will use the notation for this. I find it works best because it minimizes the chances of typos, which is a plus when we’re not aiming for artistry or fame! I will denote double negation as .

Cases	A	B
1	0	0	1
2	0	1	1
3	1	0	0
4	1	1	0

5. Possibility – TRUE statement for B

Designation:

Equation:

The TRUE statement regarding B operates in the same way as the true statement regarding A, but now the emphasis is on statement B‘ I’ll sing during the math lecture—and at this point, it doesn’t matter where the lecture falls on the boredom scale. Once the urge to sing hits, there’s no holding back!

Cases	A	B
1	0	0	0
2	0	1	1
3	1	0	0
4	1	1	1

6. Possibility – NOT TRUE statement for B

Designation:

Equation: or

The NOT TRUE statement regarding B operates in the same way as the FALSE statement regarding A—what a cunning coincidence… No matter how appealing singing might be and how much everyone at the university would be talking about me, I still won’t sing, regardless of how boring the lecture is…

Cases	A	B
1	0	0	1
2	0	1	0
3	1	0	1
4	1	1	0

7. Possibility – AND

Designation:

Equation: or

The AND relationship will be true only if both conditions are met simultaneously: ‘I bet a bottle of Jack Daniels that if the math lecture is boring, I will start singing before the break.’ If I want that bottle of whiskey, I must fulfill both conditions. This relationship is also referred to as INTERSECTION and MULTIPLICATION in books.

Cases	A	B
1	0	0	0
2	0	1	0
3	1	0	0
4	1	1	1

8. Possibility – NAND

Designation:

Equation: or

The NOT-AND (NAND) relationship will be TRUE when neither condition is met simultaneously, meaning: The lecture is NOT boring, so I stay in my seat and pay attention, hoping to absorb something… The lecture is NOT boring, but I still liven things up with some singing. The lecture is boring, but I don’t feel like singing.

Cases	A	B
1	0	0	1
2	0	1	1
3	1	0	1
4	1	1	0

9. Possibility – OR

Designation:

Equation: or

The OR relationship will be true if at least one of the conditions is met, or if both are TRUE at the same time. This operation is also known as UNION and ADDITION

Cases	A	B
1	0	0	0
2	0	1	1
3	1	0	1
4	1	1	1

10. Possibility – NOR

Designation:

Equation: or

The NOR relationship is the negation of the OR relationship; it will be true if neither statement occurs simultaneously. Notice that this is essentially the inverse of the NOT-AND operation!

Cases	A	B
1	0	0	1
2	0	1	0
3	1	0	0
4	1	1	0

I intentionally separated the table in this way because now we’re diving into IMPLICATIONS—meaning we’re taking a step up the path of mathematical logic. An implication can also be referred to as a consequence. This operation always involves at least two logical statements, where the first statement is the premise (antecedent), and the second is the conclusion (consequent), from which we draw our inference. The statements A and B still mean the same thing.

I’ve taken this section separately because it’s where most misunderstandings arise in everyday life. Just look at a reading comprehension test; these structures are everywhere. Now, let’s explore the remaining 6 cases…

11. Possibility – Implication (IMPLY)

Designation: or or

Equation: or or vagy

IMPLICATION takes the form of a structure like ‘if… A, then… B.’ From a FALSE statement (A=0), the consequent can either be FALSE (B=0) or TRUE (B=1). However, from a TRUE statement (A=1), the consequent cannot be FALSE (B=0); it can only be TRUE (B=1). For example: ‘If the math lecture becomes boring, then I will start singing.’

Cases	A	B
1	0	0	1
2	0	1	1
3	1	0	0
4	1	1	1

12. Possibility – Non-Implication (NIMPLY)

Designation: or or

Equation: or or vagy

The NON-IMPLICATION takes the form of ‘it’s not true that… if A, then… B’. This negation of the previous operation only becomes TRUE when a TRUE statement (A=1) leads to a FALSE consequence (B=0)! This fascinating logical relationship is also known as SUBTRACTION.

Cases	A	B
1	0	0	0
2	0	1	0
3	1	0	1
4	1	1	0

13. Possibility – Converse Implication

Designation: or or

Equation: or or vagy

The CONVERSE IMPLICATION has the structure of “if not B, then not A.” From a FALSE consequence (B=0), either a FALSE statement (A=0) or a TRUE statement (A=1) can follow. However, from a TRUE consequence (B=1), a FALSE statement (A=0) cannot arise; it can only yield a TRUE statement (A=1). For example: “If I do NOT sing, then the math lecture cannot be boring.”

Cases	A	B
1	0	0	1
2	0	1	0
3	1	0	1
4	1	1	1

14. Possibility – Converse NON-Implication

Designation: or or

Equation: or or vagy

The CONVERSE NON-IMPLICATION takes the form of “it’s not TRUE that if not B, then not A.” For example: ‘it is not true that if I don’t start singing, then the math lecture isn’t boring.” In competency tests, this often leads to the question of when this statement is TRUE.

Cases	A	B
1	0	0	0
2	0	1	1
3	1	0	0
4	1	1	0

Finally, let’s explore antivalence and equivalence. No, these are not third-tier Spanish football teams. Equivalence is, in mathematical terms, a notion of identity; in plain language, it refers to the equality of two things. Antivalence, on the other hand, is the opposite of equivalence. It’s straightforward, isn’t it? I tell you, mathematical logic isn’t hard at all. Let’s take a closer look at them…

15. Possibility – EQUIVALENCE (BICONDITIONAL)

Designation: or

Equation: or or vagy

EQUIVALENCE is characterized by the phrase “if and only if.” In this case, both conditions are either TRUE at the same time or false at the same time. For example: “I will sing if and only if the math lecture is boring,” or alternatively, “I do not sing if and only if the math lecture is not boring.”

Cases	A	B
1	0	0	1
2	0	1	0
3	1	0	0
4	1	1	1

16. Possibility – ANTIVALENCE (EXCLUSIVE DISJONCTION)

Designation: or or

Equation: or or vagy

ANTIEQUIVALENCE represents a “either-or” situation. In this case, ONLY one of the conditions can be true. For example: “Either I will sing, or the math lecture will remain boring.” A math teacher might think that this could shake things up and engage the audience!

Cases	A	B
1	0	0	0
2	0	1	1
3	1	0	1
4	1	1	0

I assume that’s quite enough for today. However, we had to get through this; this table is the foundation of all mathematical logic. With this understanding, grasping the axioms will be much easier… In the next entry, we will delve into the axioms of Boolean algebra!