In the previous entry, we examined the foundations of mathematical logic. Now, let us explore the axioms of Boolean algebra, accompanied by derivations—because I believe that understanding is greatly enhanced when we can see the derivations and understand how each element follows from the others.
Axioms of Boolean algebra
I think it’s important to first explain the meaning of the term “axiom.” An axiom refers to a self-evident truth that is accepted as fundamental within a given framework, which means it does not require proof or further explanation —much like the fact that none of my cats can operate a submarine. However, I believe a more profound understanding is achieved when one can see the proof behind a concept. We have a total of 11 axioms to explore in mathematical logic, but don’t worry; none of them are difficult; they are almost self-evident
I. Axiom – Associativity law
This axiom can be expressed in two forms:
- Form 1:
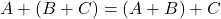
- Form 2:
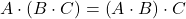
Associativity signifies the ability to group expressions, meaning you can re-parenthesize without affecting the result! For our proof, I’ll be using Form 2. Let’s dive into the truth table—it’s about to get thrilling with three terms! These are simple multiplications, and I’ll detail each step along the way.
The task: ![]()
| Options | |||||||
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 |
If you’ve now examined the last two columns of the table, you will notice that they are completely identical, which means we have successfully proven the form ![]() . The Hungarian-American mathematician Paul Halmos introduced the symbol (
. The Hungarian-American mathematician Paul Halmos introduced the symbol (![]() ) at the end of the proof (1916-2006). I will include this symbol at the conclusion of every derivation. The proof of the form ( A + (B + C) = (A + B) + C ) can be demonstrated in a similar manner.
) at the end of the proof (1916-2006). I will include this symbol at the conclusion of every derivation. The proof of the form ( A + (B + C) = (A + B) + C ) can be demonstrated in a similar manner.
II. Axiom – Commutativity law
Translated into English, this means that the order of the individual factors in an expression can be swapped without changing the result! How exciting! We can represent this axiom in two forms:
- Form 1:
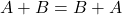
- Form 2:
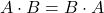
Now, let’s prove the following statement:
![]()
| Options | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
The last two columns of the table are equal, which means we have successfully proven that: ![]()
III. Axiom – Distributivity law
Multiplication is distributive over addition, meaning you can break down the parentheses—logic multiplication distributes across its terms, while logical addition is performed on each factor separately. This fundamental axiom exists in two forms:
- Form 1:
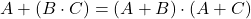
- Form 2:
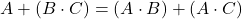
Okay, now prove the Form 1: ![]()
For the sake of simplicity, let’s use the following designations: ![]() and
and ![]()
| Options | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 |
Tbe column 6 are 9 identical, therefore ![]()
Note: the ![]() is not a type; rather a speciality of Boolean algebra. Do not interpret 1 is an ordinary number – instead, consider it as representing FALSE (0) and TRUE (1) values
is not a type; rather a speciality of Boolean algebra. Do not interpret 1 is an ordinary number – instead, consider it as representing FALSE (0) and TRUE (1) values
IV. Axiom – Complementation law
The word “complement” refers to the logical negation—that is, a statement that an TRUE assertion cannot exist without its FALSE counterpart. This principle can also be expressed in two forms:
- Form 1:
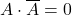
- Form 2:
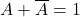
The proof:
| Options | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 |
The last two columns of the table show opposing results as options, and that was our goal. ![]()
V. Axiom – Idempotency law
Put simply, it means that I have two sets, and both contain exactly the same elements. When I take the union or intersection of these two sets—these are two-variable expressions—I always obtain the same result every time.
- Form 1:
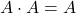
- Form 2:
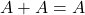
The proof:
| Options | |||
|---|---|---|---|
| 1 | |||
| 2 |
The last two columns of the table are equal to the value of ![]() in both cases, and this is what we set out to prove.
in both cases, and this is what we set out to prove. ![]()
VI. Axiom – Identity law
- Form 1:
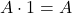
- Form 2:
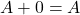
The proof:
| Options | |||
|---|---|---|---|
| 1 | |||
| 2 |
The last two columns of the table are equal to the value of ![]() in both cases, and this is what we set out to prove.
in both cases, and this is what we set out to prove. ![]()
VII. Axiom – Annulment law
- Form 1:
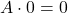
- Form 2:
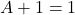
The proof:
| Options | |||
|---|---|---|---|
| 1 | |||
| 2 |
The last two columns of the table are equal to the value of ![]() in both cases, and this is what we set out to prove.
in both cases, and this is what we set out to prove. ![]()
Note: This identity can also be applied when simplifying an expression like ![]() later on. Observe that, because of the second form, the part inside the parentheses will always be equal to 1. Therefore, the expression simplifies to the form
later on. Observe that, because of the second form, the part inside the parentheses will always be equal to 1. Therefore, the expression simplifies to the form ![]() .
.
VIII. Axiom – Complement law
- Law 1:
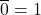
- Law 2:
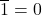
Therefore ![]() and 1 are complement results.
and 1 are complement results.
IX. Axiom – Absorption law
This is a bit more complex than the previous ones. Absorption here means that we can remove redundant terms from the expression, simplifying the problem without changing the final result. As before, this principle can be expressed in two forms:
- Form 1:
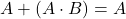
- Form 2:
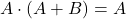
The proof:
| Options | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 |
Notice that ![]() ,
, ![]() and
and ![]() are equal.
are equal. ![]()
- Note 1:
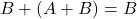 and
and 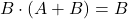 can be quickly proved using a truth table
can be quickly proved using a truth table - Note 2: The equation
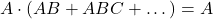 can be derived in the same way. All we need to do is factor out
can be derived in the same way. All we need to do is factor out 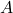 and transforming the expression into:
and transforming the expression into: 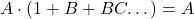 . At this point, the VI. axiom comes into play, which states that the value inside the parentheses is 1 – that is
. At this point, the VI. axiom comes into play, which states that the value inside the parentheses is 1 – that is 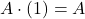
In addition to the logical proof, you should also demonstrate the absorption axiom using a truth table. Since there are two variables ![]() and
and ![]() , there are a total of 4 possible combinations for each form, so the total number of variations across all expressions is 32…
, there are a total of 4 possible combinations for each form, so the total number of variations across all expressions is 32…
![]() and
and ![]() expressions:
expressions:
| Options | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
![]() and
and ![]() expressions:
expressions:
| Options | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
X. Axiom – Double negation law
This one looks like this: ![]() .
.
The proof:
| Options | |||
|---|---|---|---|
| 1 | |||
| 2 |
The truth table clearly shows that after applying double negation, we regain the original statement ![]() .
. ![]()
XI. Axiom – De Morgan law
- Identity 1:
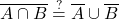 let’s rewrite it into:
let’s rewrite it into: 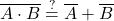
- Identity 2:
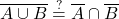 and we rewrite it this one too:
and we rewrite it this one too: 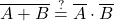
You did it! The only two things left are understanding the order of operations AND practicing it.
Order of Operations in Boolean Algebra
The order of operations is not only critically important in Boolean algebra but across all of mathematics. You’ve probably seen various posts online claiming that only “geniuses” can solve equations with parentheses. To be honest, I don’t know how long the measurement of genius has been so low that such claims are made. Anyway, the order of operations — it’s not just mathematical logic:
- Parentheses
- Negation
- AND (Conjunction)
- OR (Disjunction)
Most often, you’ll be given an expression ![]() , which you need to simplify as much as possible. In this section, you have all the necessary information to solve such logic problems. It’s not complicated if the basics are clear and you have a routine for solving these tasks. In the next part, I’ll provide exercises related to almost every example.
, which you need to simplify as much as possible. In this section, you have all the necessary information to solve such logic problems. It’s not complicated if the basics are clear and you have a routine for solving these tasks. In the next part, I’ll provide exercises related to almost every example.
If you’re heading towards electrical engineering, it gets even more complex with circuit diagrams — many inputs, switches, and then you need to draw the simplest circuit. The point of this is to use the fewest circuit components possible.
Problem-Solving Strategy
- Write down all the operations and axioms on a sheet of paper — this will be helpful when doing mathematical logic tasks — it makes debugging much easier.
- Absorption rule — become a master of it; you can save a lot of time, which is very useful during exams and quizzes.
- Work cleanly, mark everything clearly!
- Avoid using the
 symbol for multiplication — you might accidentally introduce an extra variable along the way.
symbol for multiplication — you might accidentally introduce an extra variable along the way. - Write the terms in alphabetical order: A, B, C, and so on.
- Work from the inside out — perform all operations inside parentheses first, following the order of operations, and only then remove the parentheses.
Exercises for the mathematical logic part will be provided in the next post.